画像 多角形 内角の和 一覧 328956-多角形 内角の和 一��

 こんにちは、ウチダです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください 変形多角形の 内角？考え方～ 変形多角形の 内角？ 内角の和 と 外角の和 ！ 九芒星 ？ どうやって計算するの？ 正多角形の 内角が あっという間に分かる術～ 1次関数の応用！代表問題～ 1次関数なのに、増え方が変化する 文章問題？？？？？ どうすれば n角形の内角の和 n角形の対角線の本数 読者になる おじさんの書斎 証明って、数学の一番の醍醐味だと思うんです 多角形の内角、対角線、円周角の定理、接弦定理、方べきの定理 高校数学 n角形の内角の和 n角形の対角線の本数 円周角の定理 1つの弧に対する中心角は、同じ

数学 中2 51 多角形の内角と外角の和 基本編 Youtube

多角形 内角の和 一覧

多角形 内角の和 一覧- つまり、 正多角形の1つ分の内角は、内角の和を等分することで求めれます。 例 (正三角形) 内角の和180° ⇒ 1つ分の内角 （正六角形） 内角の和7° ⇒ 1つ分の内角 外角というものを利用すると、もっと簡単に求めることができます。 が、今回は多角形の内角の和のポイント 内部につくれる三角形は、 頂点の数より2少ない！ 角形の内角の和は 十角形の内角の和は、十角 形を（ ）個の三角形に分 けることができるので、内角 の和は（ ）度となる。 ※多角形の外角の和 2 正十角形の一つの内角の大きさを求めなさい。 (1) 六角形の内角

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

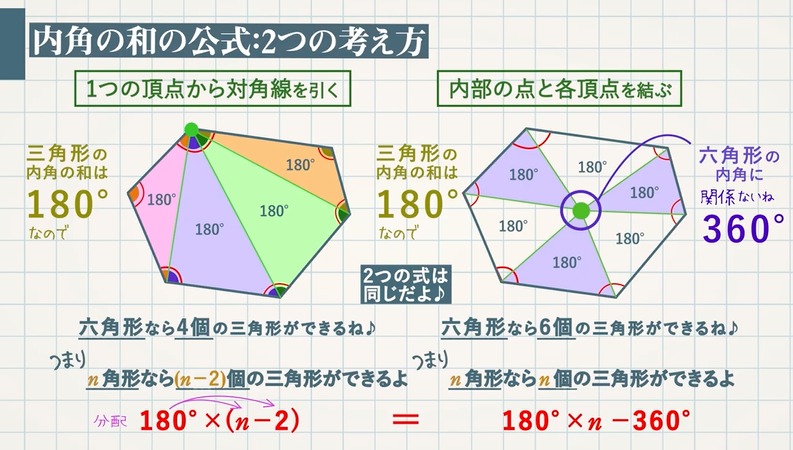
「多角形の内角の和 」を （内角の和は，180゜に三角形の個数 n を掛け，中心の 360゜をマイナスして得られる。） また,「1＝拙，2＝巧」を主題化するためには，nを6以上にする必要があります。 （5角形では，「一つの頂点から残りの頂点に対角線を引く」しかありません。） 方法2と3は，n補助（延長）線を引いて内角の和などを利用して求まります。 こういう形をした多角形を凹多角形といいますが、気にしなくて良いです。 笑 四角形や三角形に分けて、分かる角度を書き込んで行けば簡単に求まります。 赤線の補助線を入れると四角形N角形の内角の和＝180×（n－2） この公式を忘れてしまったらどうしたらよいでしょうか？ 多角形の内角の和は求められないでしょうか？ そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。 三角形

多角形の外角の和は360°になる >>外角の和説明 例 十角形の内角の和 n角形の内角の和は180(n2)なので n=10を代入すると 180(102)=180×8=1440° 正八角形の1つの外角 多角形の外角の和はどれも360°なので 360°÷8=45° 確認 答表示 ① 十二角形の内角の和をN 角形は、 ( n − 2) 個の三角形に分割できるので、内角の和は 180 ( n − 2) ∘ です。 （詳しくは、 多角形の内角の和の公式を3通りの方法で証明する を参照してください。 ） よって、内角の和が 1080 ∘ になる多角形を n 角形とすると、 180 ( n − 2) = 1080 外角・内角の和、面積、対角線の公式と求め方 21年12月25日 この記事では、「多角形」についてわかりやすく解説していきます。 多角形に関するさまざまな公式（外角の和・内角の和、面積、対角線の本数など）や求め方を説明していくので、この記事

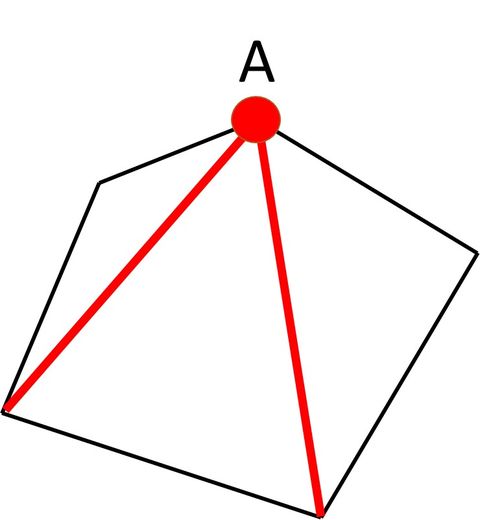
多角形の内角の和と問題の求め方 十角形の内角の和を求めましょう。 辺の数が分かれば上記の公式を使って簡単に解ける問題です。 n=10なので 多角形の内角の和=180× n－2=180× 8=1440° 内角の和と三角形の関係は？ 1分でわかる和の値、証明、外角との関係また，次の図のような図形（ここでは，「五芒星 （ごぼうせい） 型」と呼ぶことにします。 ）において，内角の和∠a∠b∠c∠d∠eについて考えます。 図のように，AC，ADとBEとの交点をそれぞれF，Gとします。 FCE， BDGに着目して，それぞれ外角の定理2 多角形の内角の求め方 多角形の内角の和の求め方については，小学校第5学年と中学校第2学年に学習することになっている。 その指導の基本的な考え方になっているのが，三角形に分割して内角の和を求めることである。 「中学校学習指導要領（平成29

小学校5年 算数 正多角形の角の大きさ Youtube

小学5年生 正多角形 算数 Active Learning 学院

 中2数学「多角形の内角の和の定期テスト過去問分析問題」です。 n角形の内角の和 内角の和＝180（n2）° 1つの内角 1つの内角＝180° 1つの外角（となりあう外角と内角は180°）です 内角と外角 ABCと辺BCを延長した直線上の点をDとします。 このとき、∠ まず、多角形の内角の和を計算する簡単な公式がこれです。 n角形の内角の和 = 180 × (n – 2) この多角形の内角の和についてなるべくシンプル簡単に紹介していきます。 基本的な図形の内角の和は皆さん知っていると思います。 （三角形の内角の和） = 180°幼稚園一覧 綾部市の じゅんじょ（小4） 式と計算（小5） 面積（小5） 文字と式（小5） 一次方程式（中1） 多角形の内角の和 （中2） 小中連携の在り方 小中連携のポイント 小中連携の対応表 小中連携の実践例 比例（小6） 二次関数（中3） まとめ 関数トランプ ダウンロード みんなの笑顔

正ｎ角形の内角の和は2 ｎ 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

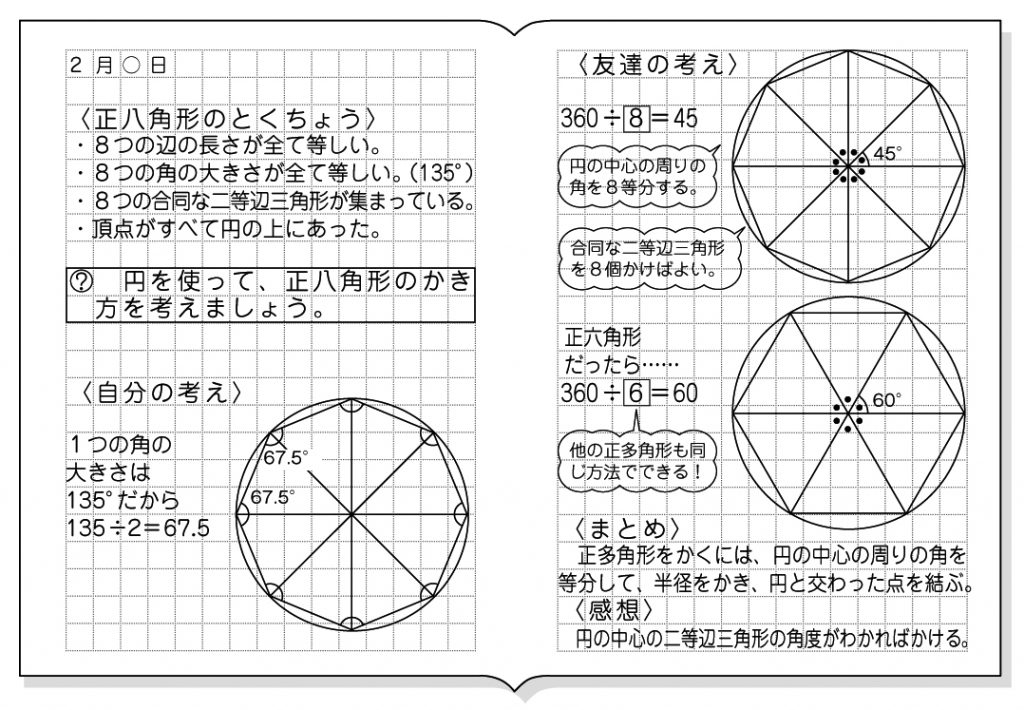
小5算数 正多角形と円 指導アイデア みんなの教育技術

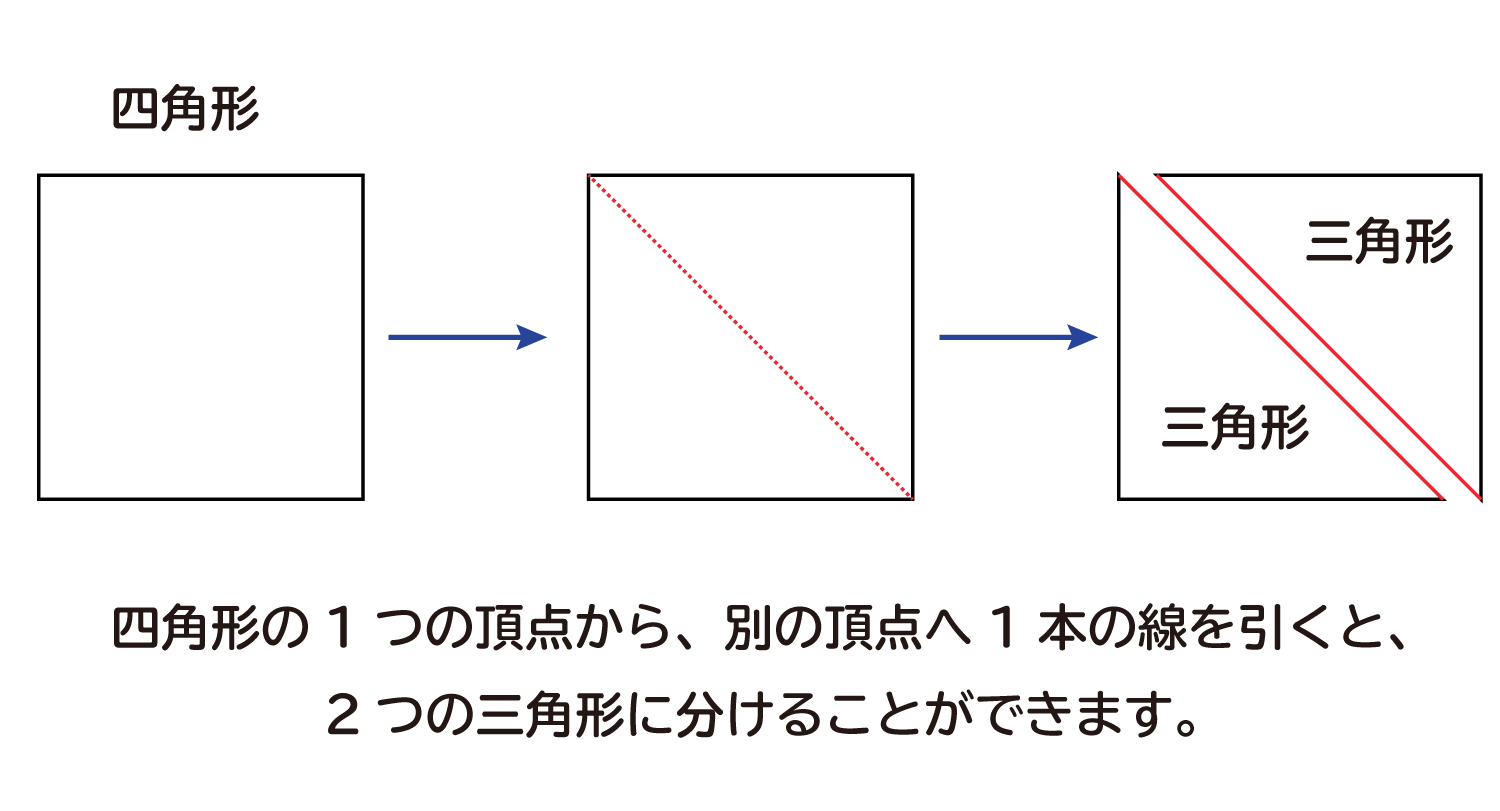
中学2年生の数学で習う多角形の外角・内角の和についての解説と問題演習です． ← pc用は別頁 外角,多角形 多角形の外角 図 1 図1のように、多角形の1つの辺とこれに隣接する辺の延長とがなす角を外角という 外角は内角の補角である (内角)(外角) =180° (外角) =180°− (内角) 図 2 よくある8動画コンテンツ一覧 0000 多角形の内角の和 0610 一般的に「n角形」の内角の和は？ 0950 なぜ（n2）なのか？（補足） 1645 多角形の外角の和は？ 2438 必ず360°になることを証明してみる（補足） 2910 練習問題★ ※練習問題で、計算が簡単になるコツや、外角に目を向けると楽という解き多角形の内角の和をいとも簡単に答えることができます それは、 多角形に対角線を引いて三角形を作る！ という作業で見つかります ↑このようにして、線を引くと、 三角形 ができますね。 そして、三角形の内角の和は、 180° ですので、 四角形なら

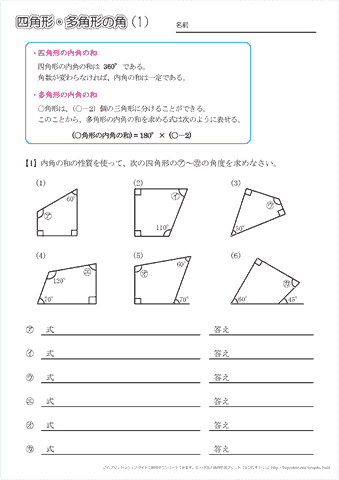
小学５年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生

多角形の内角の和 算数の公式覚えてますか

 多角形の用語（五角形・六角形・八角形・12角形・正多角形など）は、 英語でなんていうのかを この記事で図と共に紹介してい 英語独学マスター ホーム;の内角の和はいくつになるのでしょうか。 角形の内角の和の公式＝180× ( －2) ※ 絶対に覚えておいて下さい。 2 正 角形の1つの内角の大きさを求める！ 正三角形の1つの内角の大きさは60度 , 正四角形 (正方形)の1つの内角の大きさは90度です。 五角形で、内角の和が分かります。 正多角形は全ての角の大きさが同じなため、 内角の和÷角の個数 で求めることができます。 この角の個数が、正〇角形に当てはまる数になっていることも、このプリントではわかりやすく習熟できます。 正多角形のひとつ

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

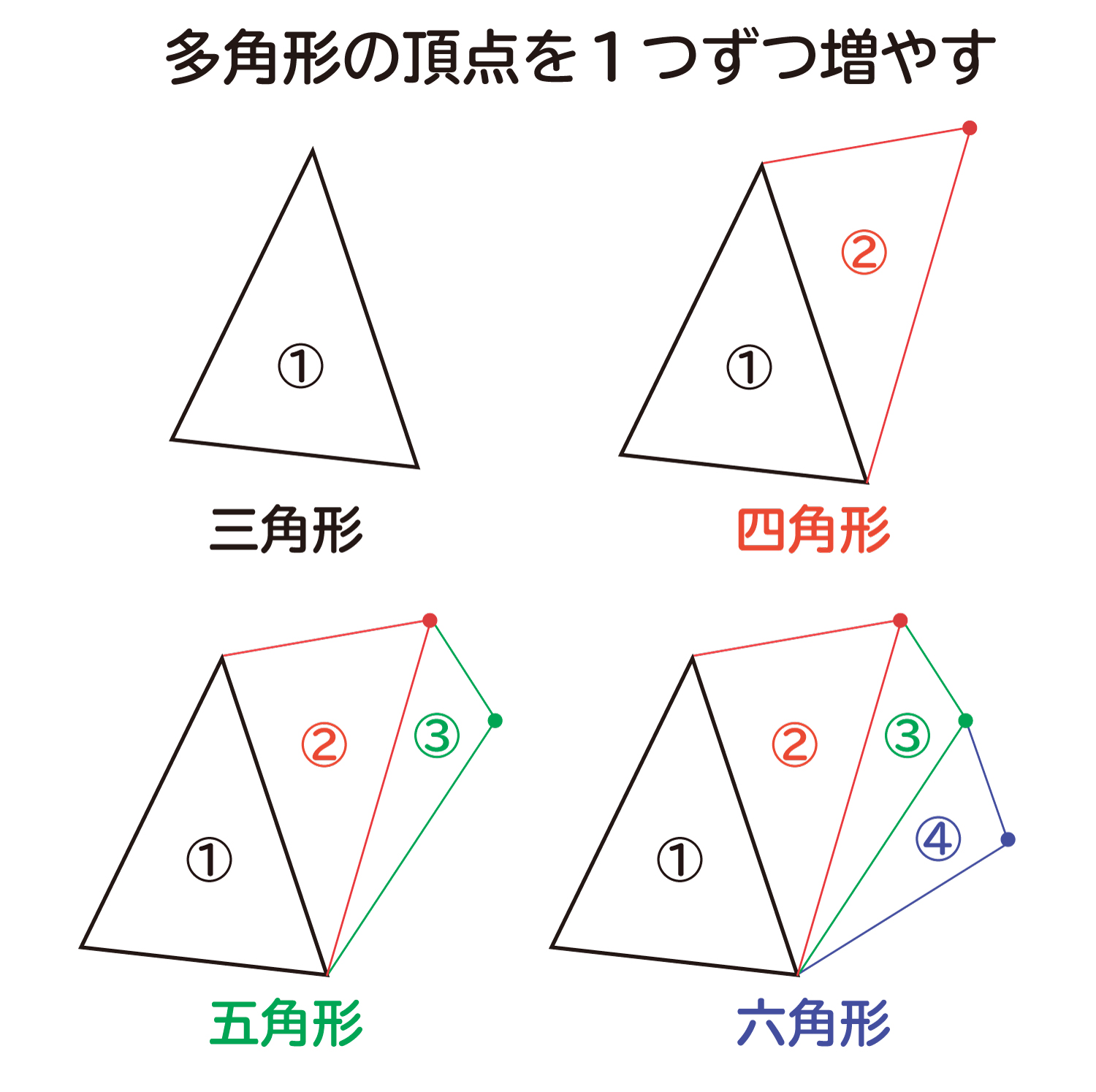
正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com

解き方はばっちりだと思いますが、別の問題と混ざっているときでもすらすら解けるように、練習してみてください。 まとめPDF「図形の角11多角形の内角」 PDF まとめPDFは、下記の16件（全32ページ）のプリント一覧をまとめて表示します。 例えば「 角形の内角の和が1440°であるとき， はいくつか？」という問題はどのように解くか？ 上の表から10になりますが，もっと大きな数になったときは次のように解きます． 出典 フリー百科事典『ウィキペディア（Wikipedia）』 ( 1100 UTC 版) 多角形の内角の和／外角の和 n 角形の内角の総和は、多角形の形状に関わらず（凸であれ凹であれ） である。 これはどのような多角形でも、対角線で適当に区切ることで (n2) 個の三角形に分割できることから導かれる。

実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note

多角形の内角の和 計算が簡単にできる電卓サイト

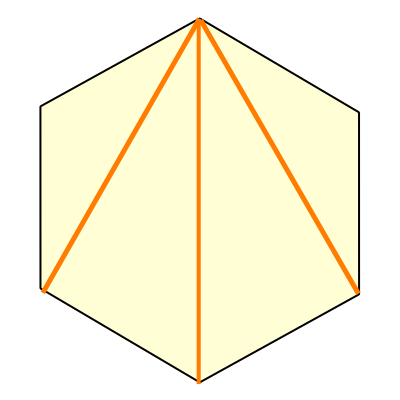
多角形の内角の和を求める公式 内角の和=180× (頂点の数2) この公式の理屈としては、まずひとつの頂点から両隣を除いた他の頂点に線を引きます。 例として六角形でおこないます。 すると、六角形の中に三角形が4つできたことになります。 両隣の頂点1つの内角を求める2つの方法 それでは、次に内角を求める方法について考えていきましょう。 正多角形の内角1つ分を求めるには2つの方法があります。 外角を利用する方法 内角の和を考える方法 それぞれの方法について解説していきます。多角形は頂点が1つ増えるごとに、中にできる三角形の数も1つずつ増える ことが分かります。 そして 三角形の数は（頂点の数ー2） の数になっていることが分かります。 多角形の内角の和は「180°×三角形の数」 で求めることが出来るので、 n角形の内角

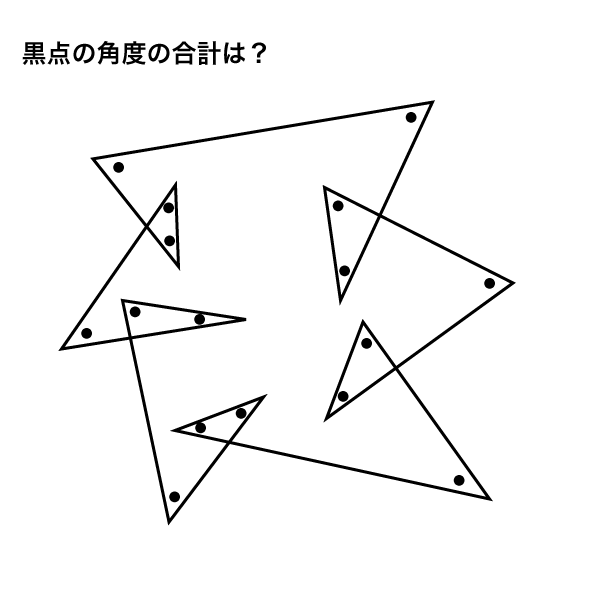
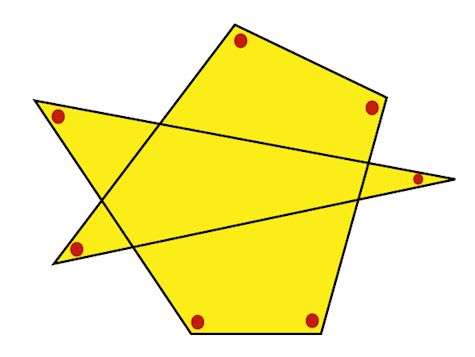
角度情報がない図形の合計の角度 星形多角形

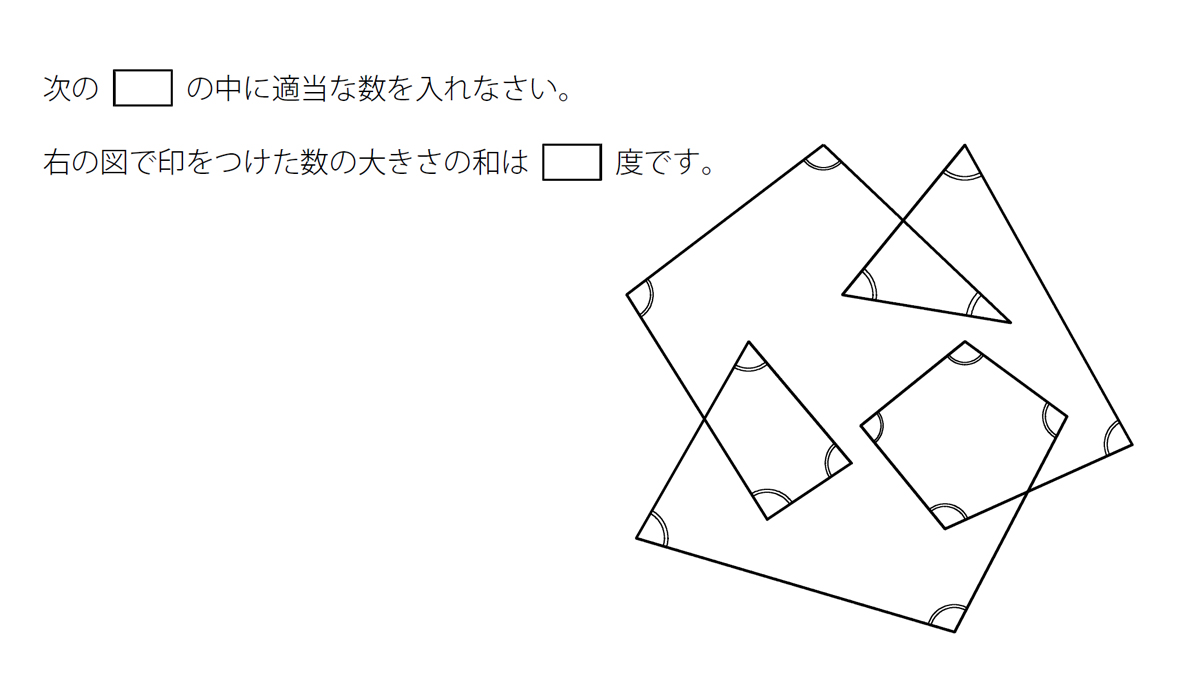
みんなの算数オンライン 最新 甲陽学院中学校から 新５ 6年生向けです 星型多角形の内角の和に関する問題です よく出る割りには正答率も低い これは解法暗記系ですね 解説はこちら T Co Qcxoawsqen 中学受験 算数 甲陽 みん算過去

多角形の内角の和 解説 三角形，四角形，五角形など，いくつかの線分で囲まれた図形を多角形といいます。 対角線は頂点と頂点を結ぶことにより引くことができますが，自分自身と自分の隣の頂点には対角線を引くことができません。つまり，n角形の場合，n個ある頂点から3個の頂点を三角形の内角の和180°を使って多角形の内角の和を考えます。 一つの頂点から他の頂点に補助線を引いて三角形に分けます。 >>クリック 四角形 →三角形2つに分けられる →三角形3つに分けられる 五角形 →三角形4つに分けられる 六角形 四角形の内角の今回は数学の話である。 多角形とは辺の数が3以上の図形であり、辺の数が増えれば増えるほど、だんだん円に近付いてくる図形である。 其の為、多角形は複数個の三角形に切る事が可能である。 其の為、多角形の内角の和は 180（n－2） という等式で

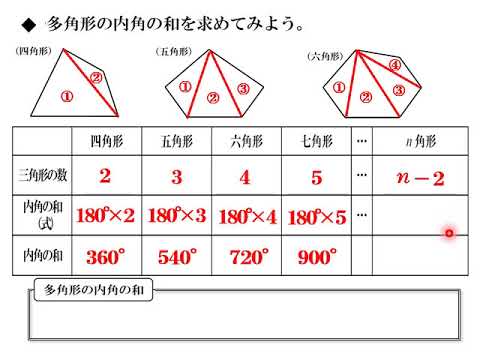
動画 多角形の内角の和 Youtube

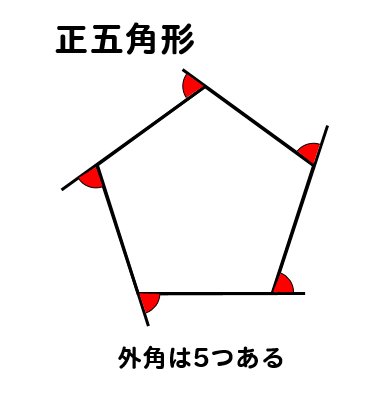
内角の和 180 N 2 外角の和 360 教遊者

 多角形の内角の和を求める公式 多角形の内角の総和は、上記のように補助線を引いて三角形がいくつできるかで知ることができます。また、上記のことから、以下の公式を導くことができます。 中学生に向けての予習 中学生になると、180° のことを記号 π ( パイ ) を使って表すように

Studydoctor多角形の内角の和 中２数学 Studydoctor

多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト

多角形の内角と外角 思考力を鍛える数学

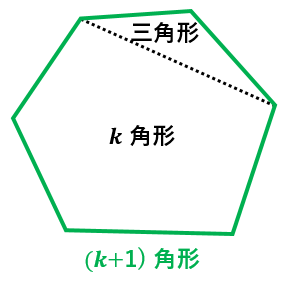
多角形の内角の和の公式を３通りの方法で証明する 具体例で学ぶ数学

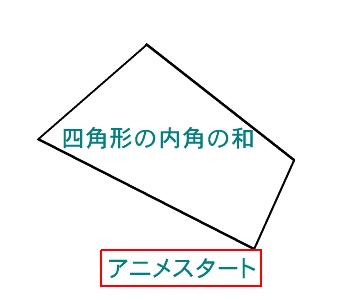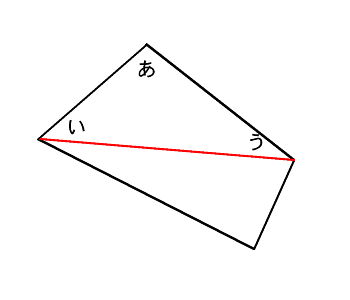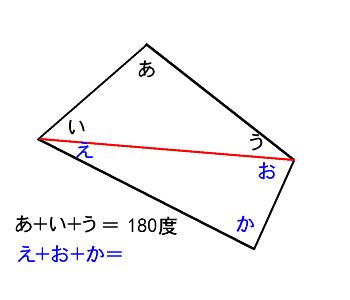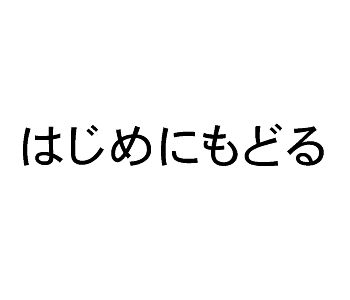
5年算数 多角形の内角の和 教え方

中２ 平行と合同4 多角形と角 Youtube

多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典

多角形の内角の和 は何度なのか を説明します おかわりドリル

多角形の内角の和はなぜ ｎ ２ のぶちゃん先生の花まる教室

多角形の内角の和を簡単に求める方法 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学

多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun

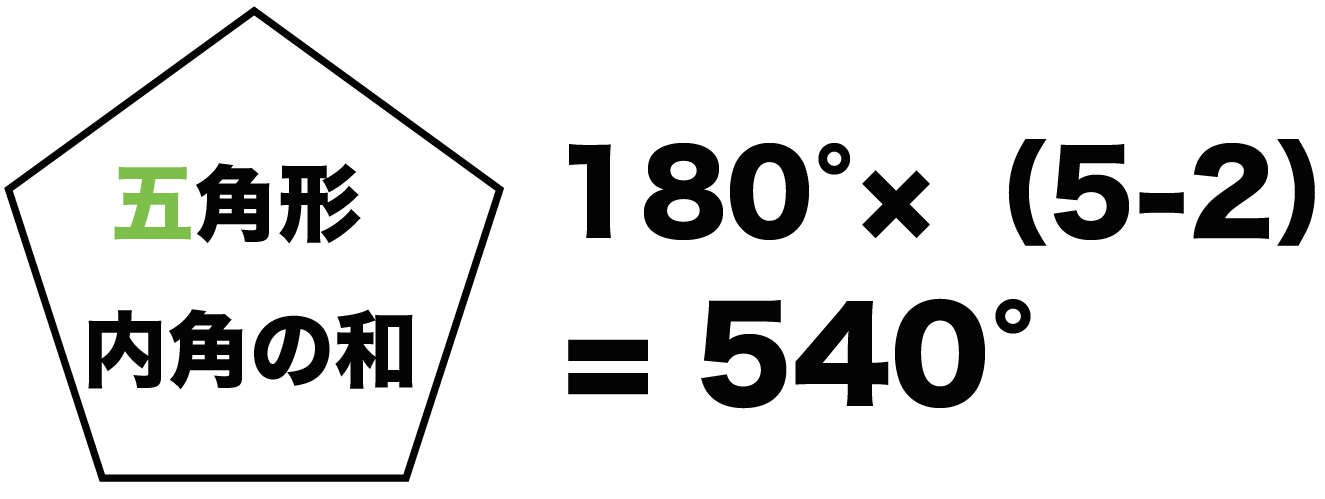
中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun

1

多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト

正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より

正多角形の内角と外角の大きさ 具体例で学ぶ数学

正多角形の1つの内角 外角を求める方法を問題解説 数スタ

多角形の性質 中学受験準備のための学習ドリル

中学受験 平面図形 多角形の内角の和を求めるには さんすうがく

内角の和 と 外角の和 名寄 算数数学教室より

多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

内角の和 180 N 2 外角の和 360 教遊者

中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu

基本のpolygons 多角形 の英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強

簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく

3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく

課題学習の指導 数学

中2数学 複雑な多角形 角の和 応用問題

変形多角形の 内角 名寄 算数数学教室より

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題

中学2年の数学 動画 多角形の内角と外角の和 基本編の問題 19ch

多角形 の内角の角度 計算ドリル 問題集 数学fun

3

ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス

多角形の内角の和 は何度なのか を説明します おかわりドリル

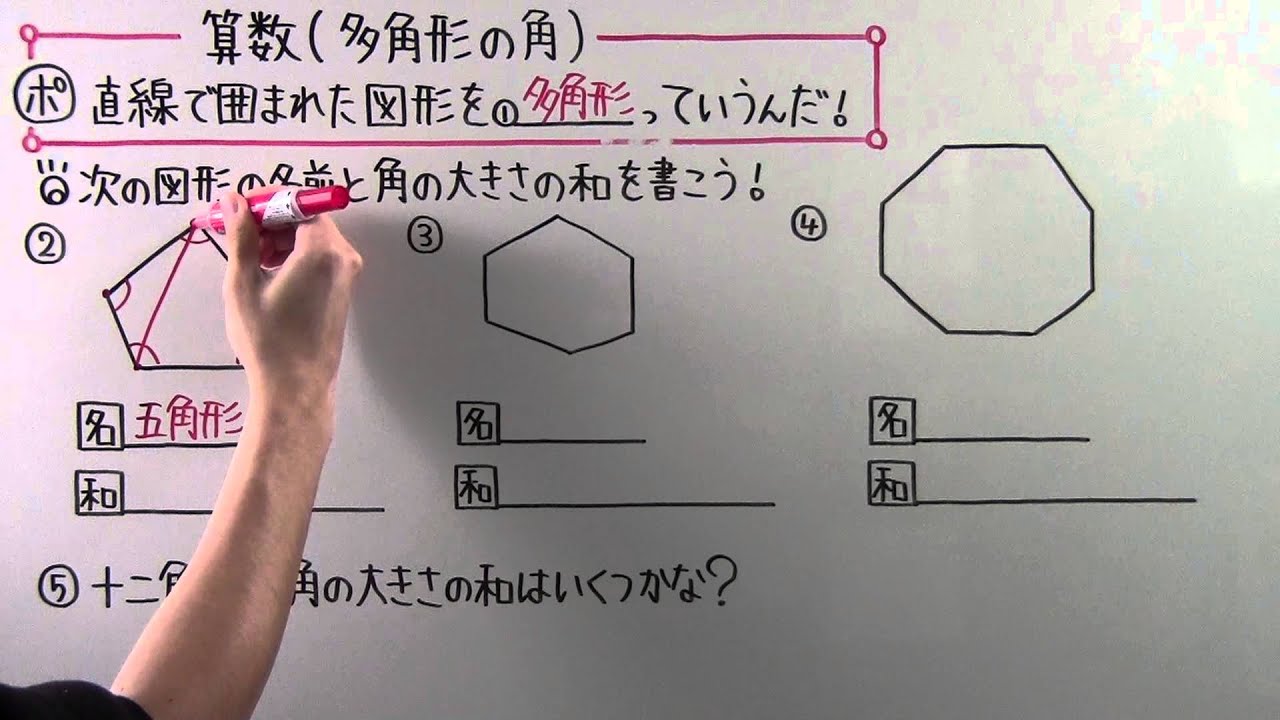
小５ 算数 小５ ３３ 多角形の角 Youtube

1

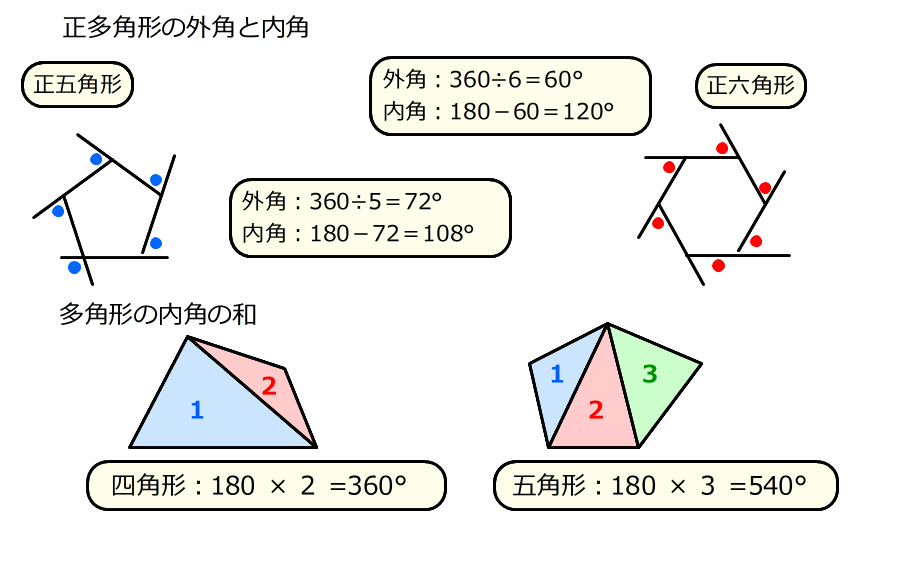
正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

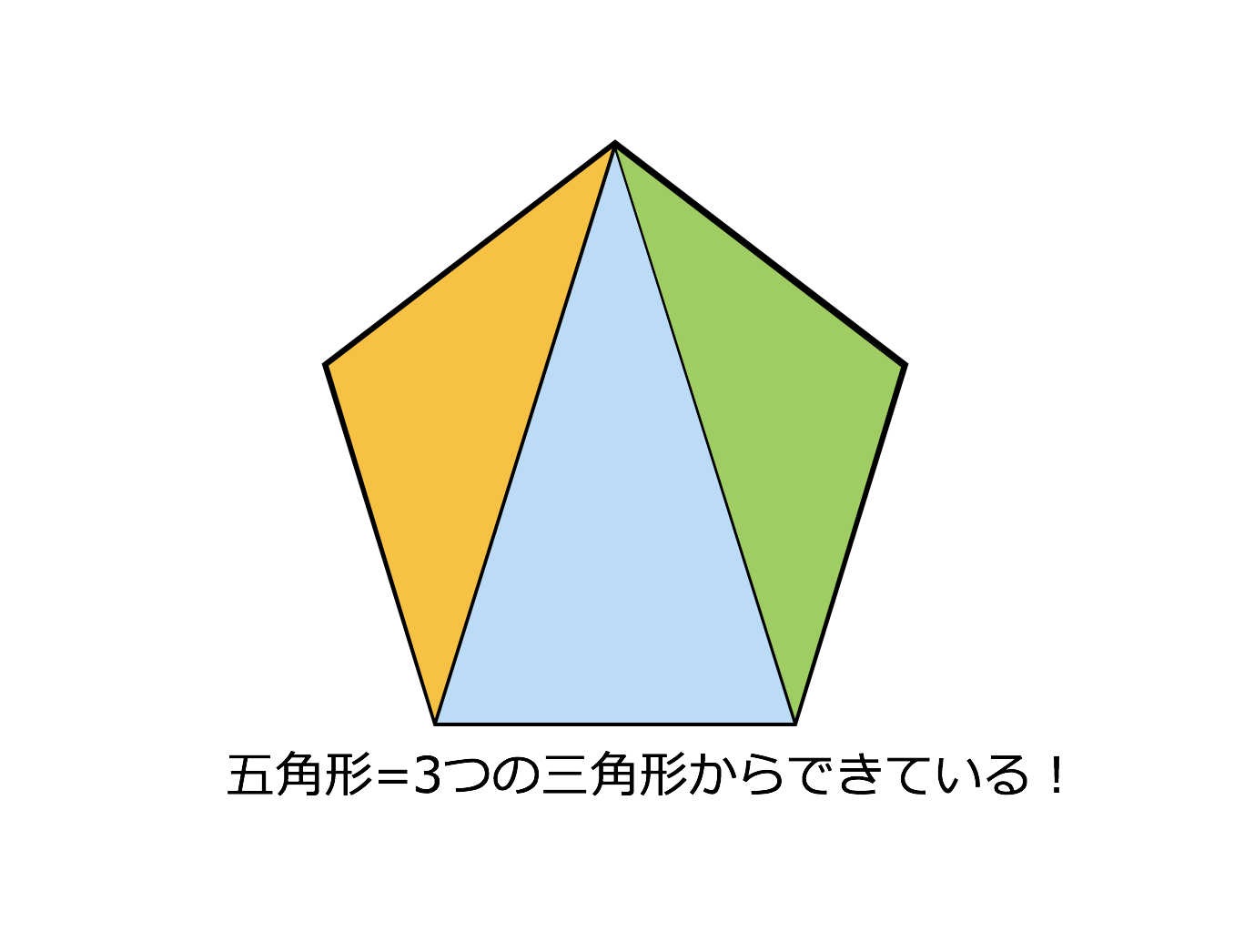
3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ

多角形の内角の和の公式と外角の和を利用した角度の求め方

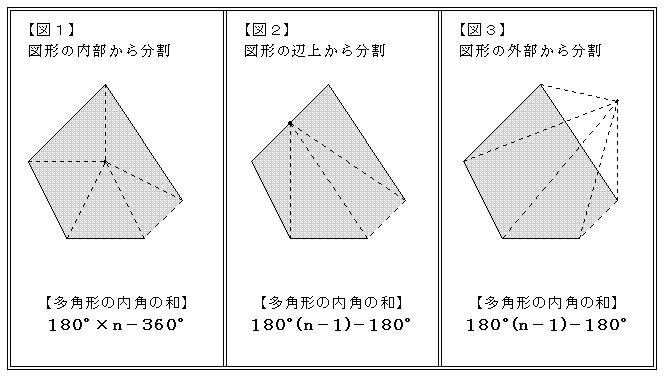
多角形の角

多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト

多角形 中学受験 の問題31題をただひたすら解くページ チャンプルー

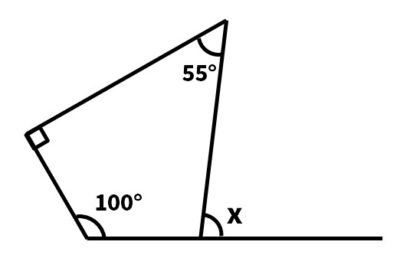
中2数学 多角形の内角の和の定期テスト過去問分析問題 ダイスト

数学 中2 51 多角形の内角と外角の和 基本編 Youtube

正六角形 正6角形 の角度の求め方は 1分でわかる値 内角の和 外角 正多角形の角度の求め方

基本のpolygons 多角形 の英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強

中2数学 複雑な多角形 角の和 応用問題

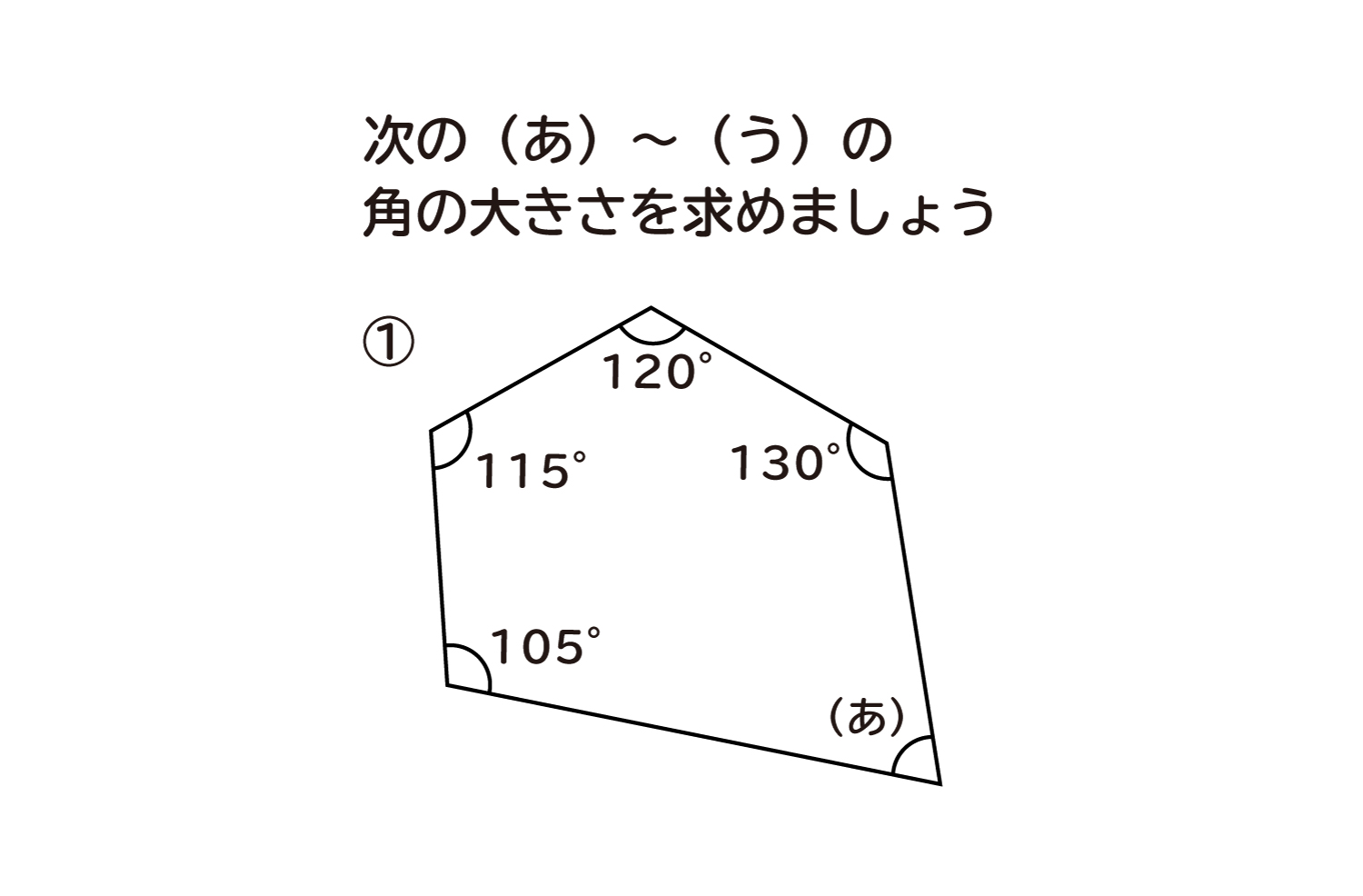
小学5年生 算数 無料問題集 多角形の角の大きさ おかわりドリル

三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

内角の和 180 N 2 外角の和 360 教遊者

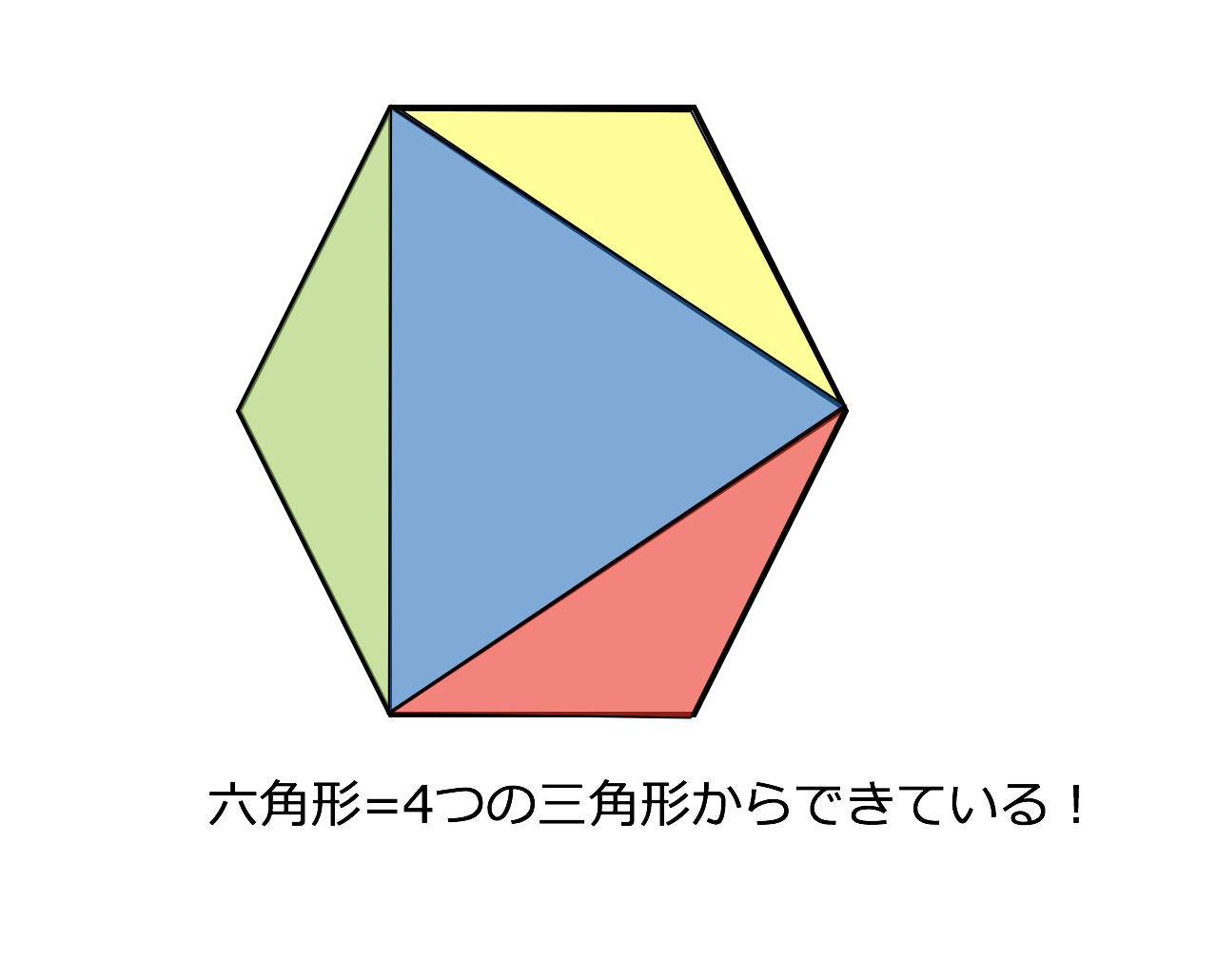
3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ

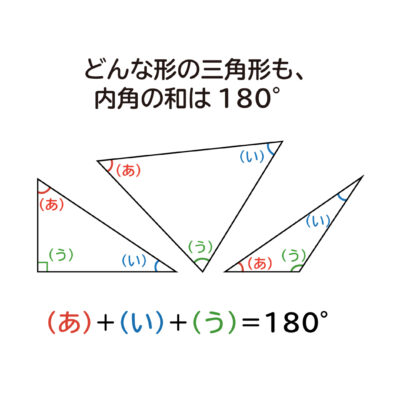
多角形の内角の和 は何度なのか を説明します おかわりドリル

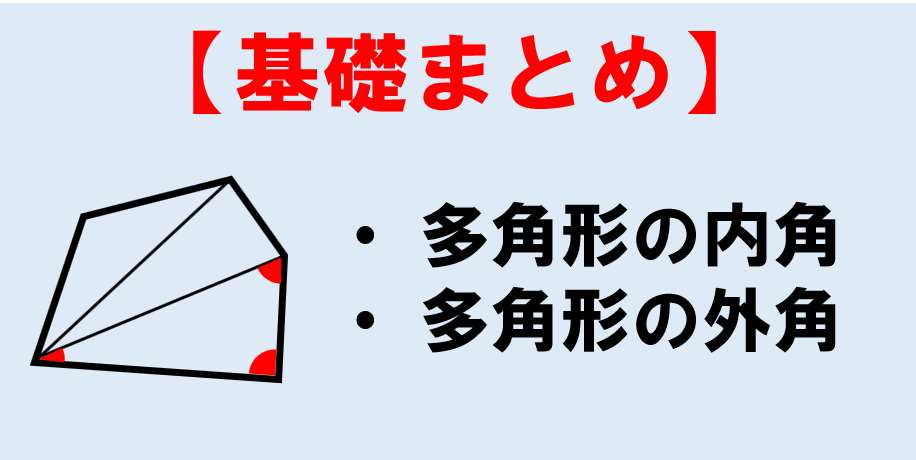
中２数学 多角形の内角の和 外角の和まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト

正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

11 8 平行線の幾何 多角形と角度問題 理一の数学事始め Note

中２数学 図形の性質と合同 多角形の内角と外角の和 Vol68 Youtube

正5角形の角度の求め方は 1分でわかる値 内角の和 正6角形 正8角形の角度は

正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典

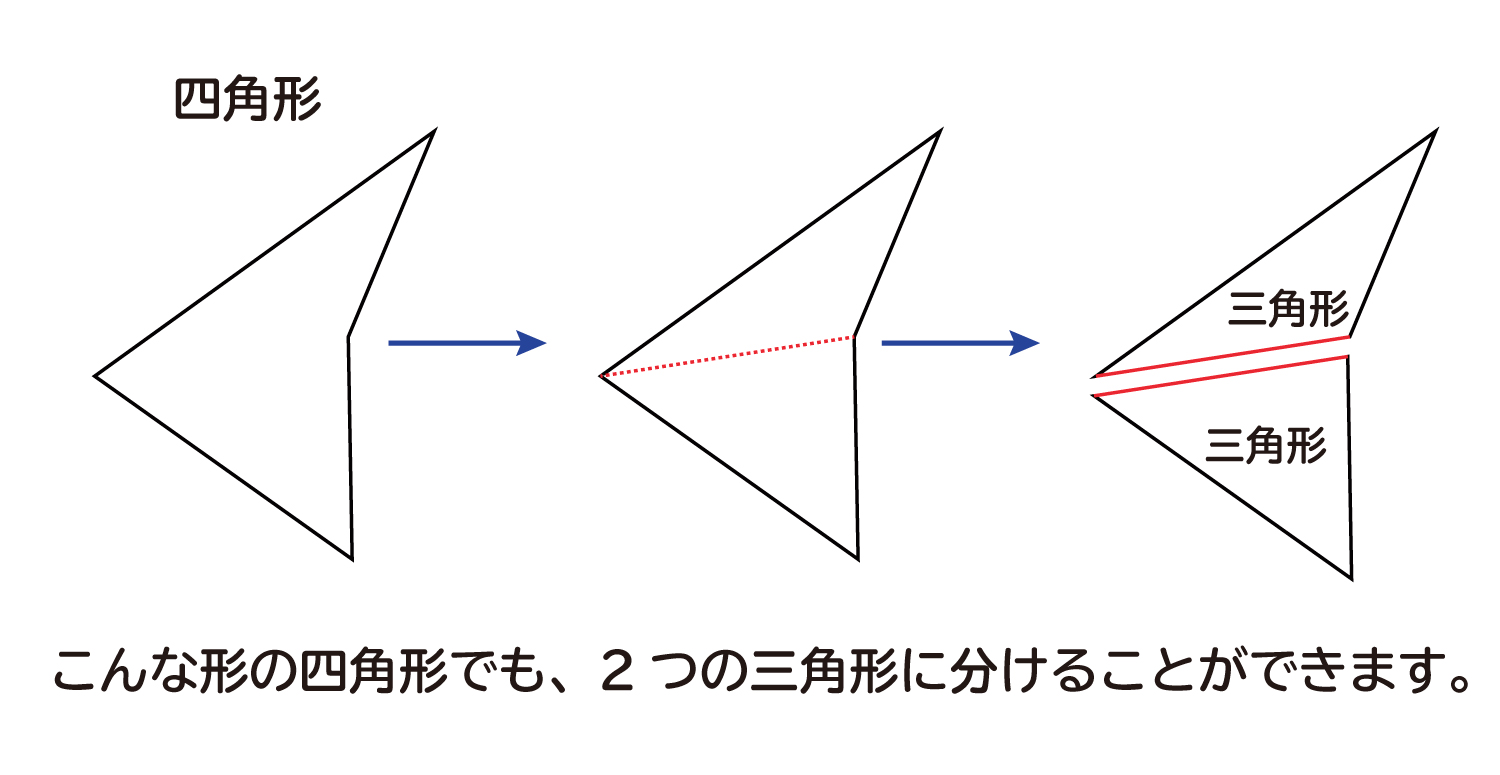
多角形の内角の和 は何度なのか を説明します おかわりドリル

1

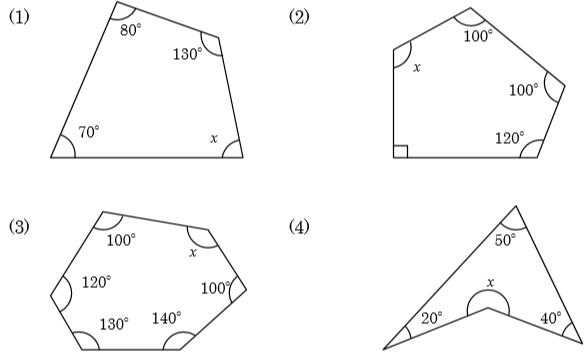
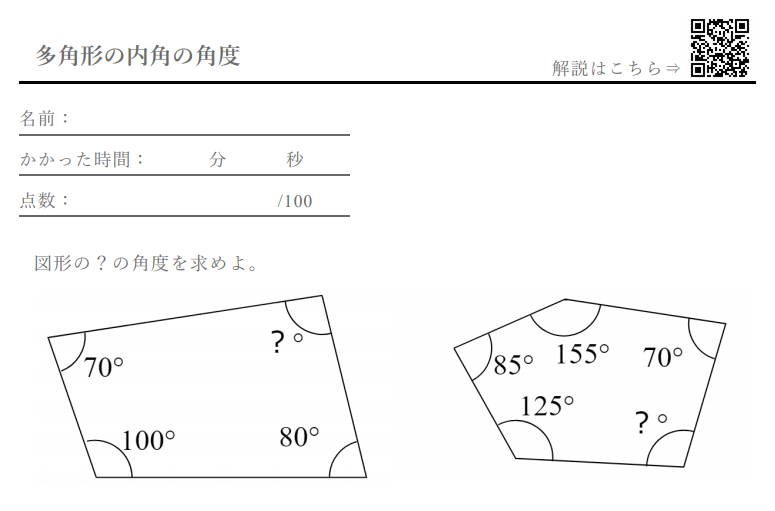
内角の和の公式 内角の和が１８００ の多角形は何角形 中学や高校の数学の計算問題

中2数学 ブーメラン型角度の求め方を解説 数スタ

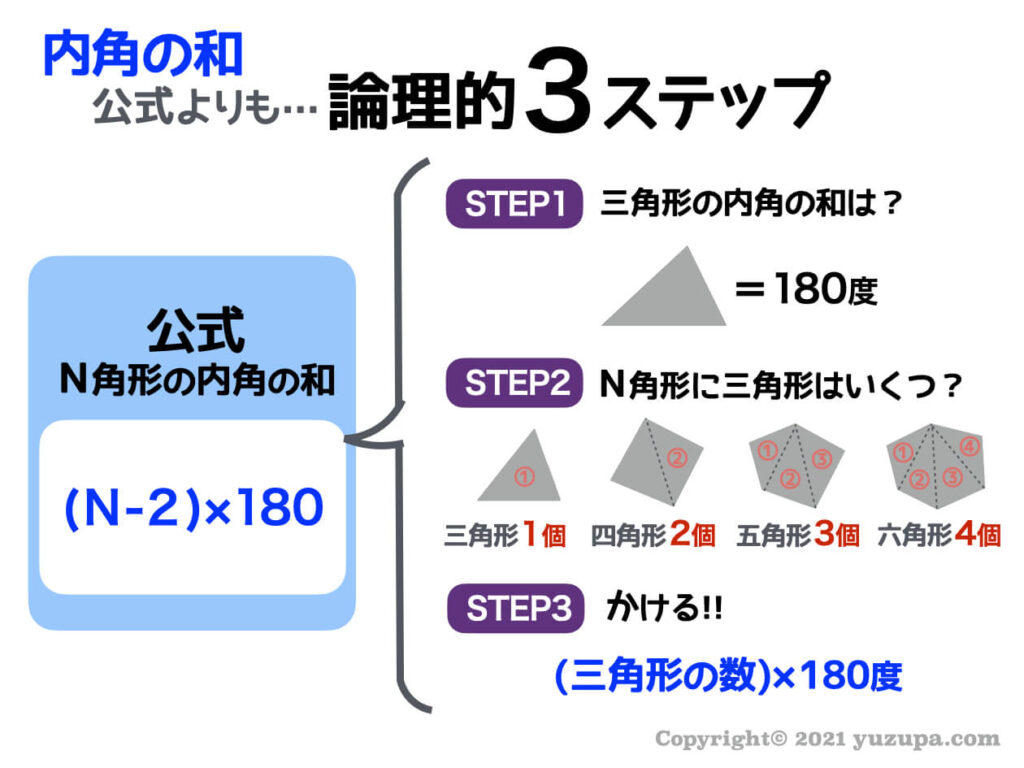
中学受験 多角形の内角の和 公式を忘れなくする論理的３ステップ かるび勉強部屋

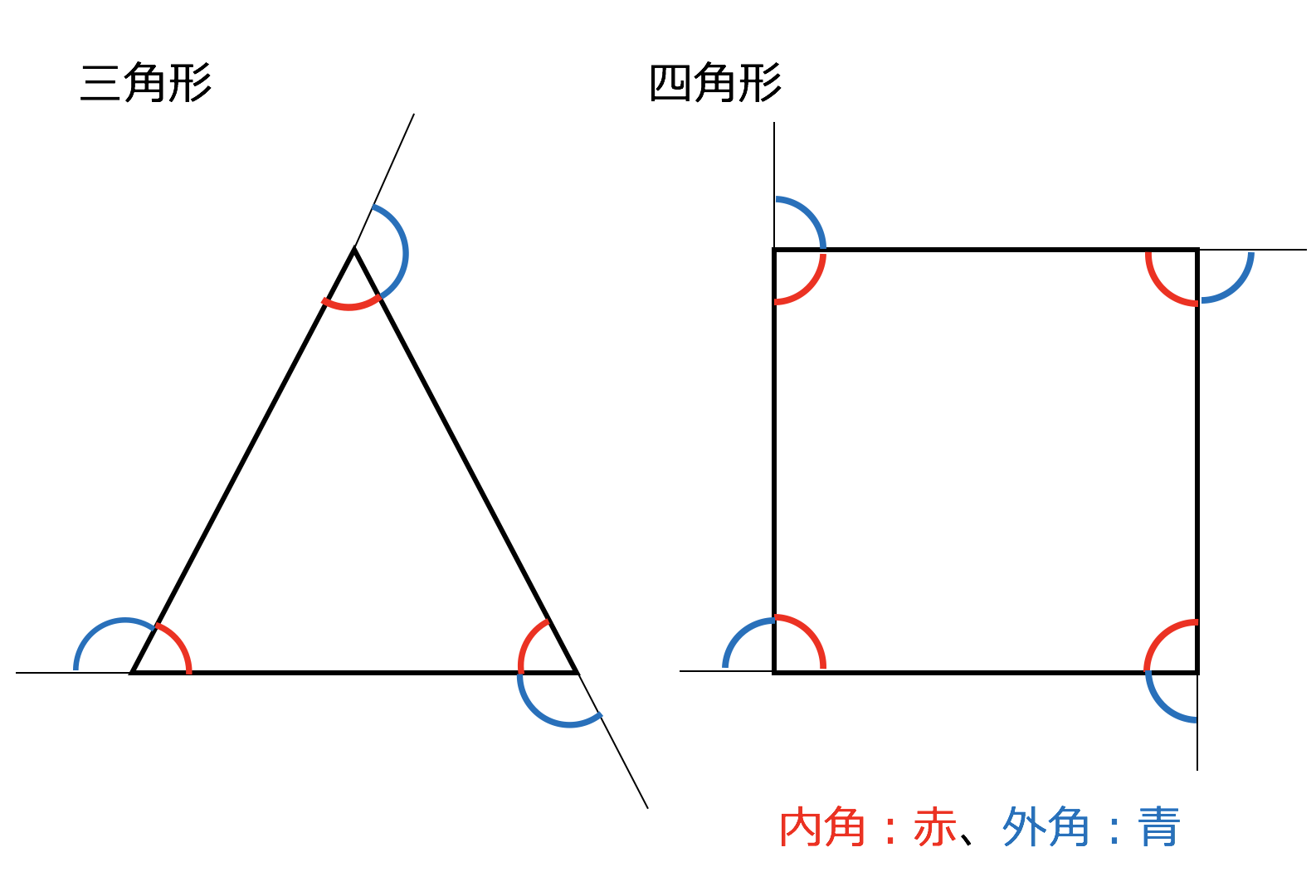
3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ

畑下 由佳 畑下由佳 Stg Origin Aegpresents Com

多角形の内角の和 は何度なのか を説明します おかわりドリル

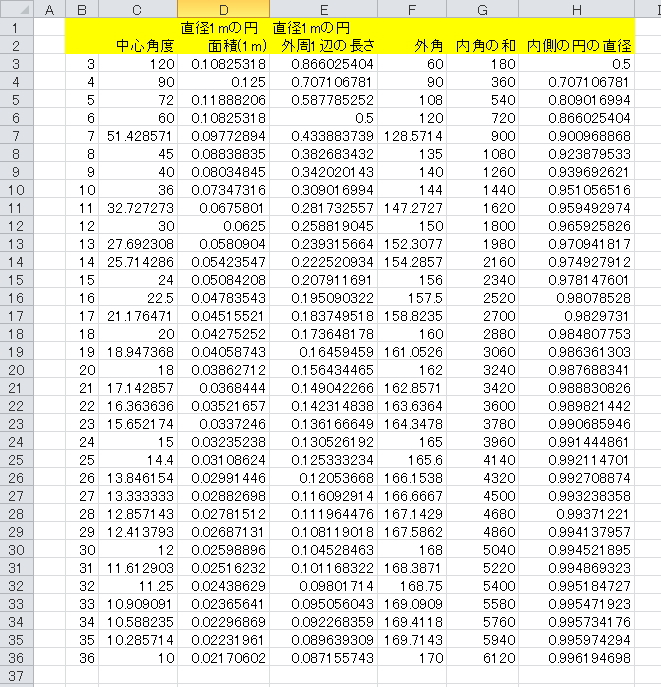
正 角形 正多角形 を表にしてみる エクセル関数の使い方

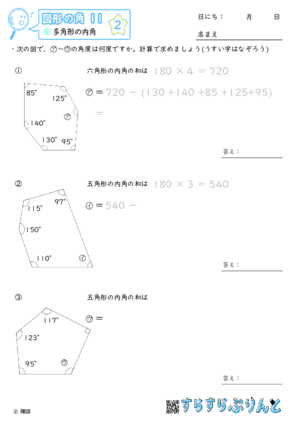
図形の角 多角形の内角 小学5年生算数 無料プリント

正多角形 Wikipedia

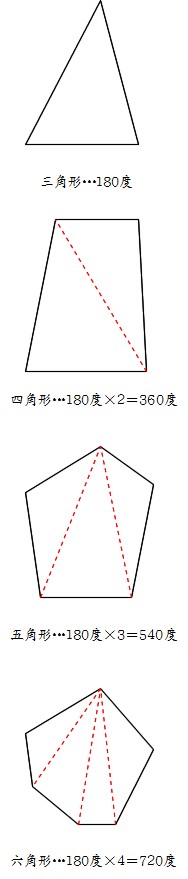
Math 多角形の内角の和 働きアリ

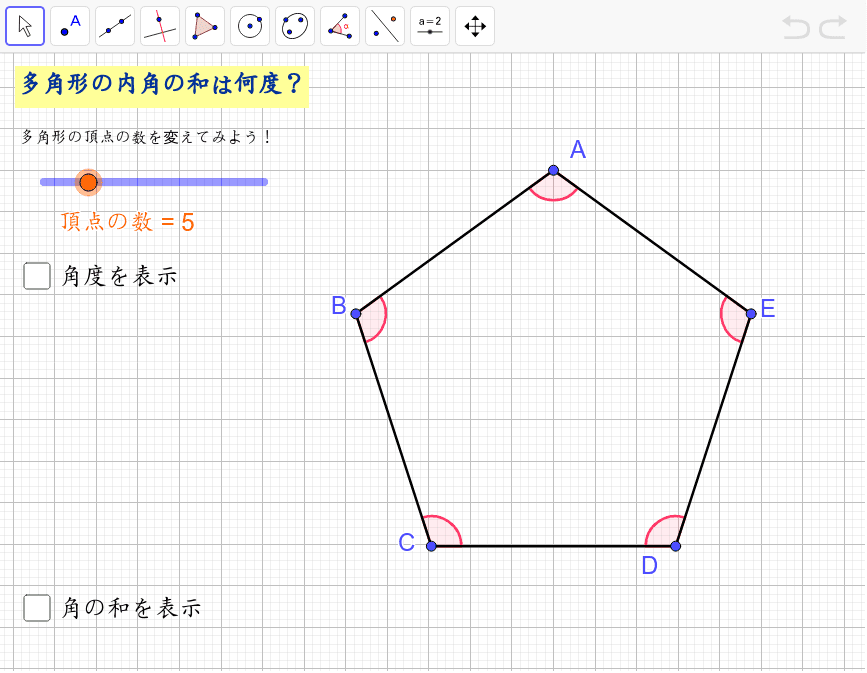
多角形の内角 Geogebra

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun

Studydoctor多角形の角度の問題 中２数学 Studydoctor

中学受験算数 多角形の内角と外角の問題 Stupedia

正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun

Incoming Term: 多角形 内角の和 一覧,